Como Resolver a Equação do 2 Grau?
A equação do 2º grau, frequentemente presente nas provas do Exame Nacional do Ensino Médio (ENEM), é um dos conceitos fundamentais da matemática.
Sua definição, ax2 + bx + c = 0, onde a, b, e c são números reais e a≠0, destaca a característica que lhe dá o nome: a variável x está elevada ao expoente 2. Este expoente é o que define o grau da equação, daí o termo “equação do 2º grau“.
Essa estrutura específica não apenas dá nome à equação, mas também influencia suas propriedades e as soluções que ela pode ter. O domínio da equação do 2º grau é vital para os estudantes que se preparam para o ENEM, pois além de ser um tópico recorrente no exame, compreender essa equação abre caminho para entender conceitos mais complexos em matemática.
Vamos agora apresentar um guia passo a passo de como resolver a equação do 2 grau.
Identificando os Coeficientes
Os coeficientes de uma equação do 2º grau são as peças que definem sua forma e soluções. Entender cada um deles é o primeiro passo para desvendar essa equação.
Uma equação do 2º grau possui a forma geral ax2 + bx + c = 0, onde a, b, e c são os coeficientes.
Por exemplo, na equação 3x2 + 5x + 2 = 0, os coeficientes sao: a = 3, b = 5 e c = 2.
Raiz de uma Equação do 2 Grau
As raízes de uma equação do 2º grau são os pontos em que a parábola cruza o eixo x, ou seja, as soluções da equação.
Para encontrar essas raízes, utilizamos a famosa Fórmula de Bhaskara:
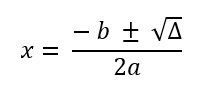
Fórmula do delta:
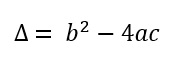
Resolvendo, Passo a Passo, uma Equação do Segundo Grau: 2x2 – 9x + 7 = 0
Quem foi Bhaskara?
Bhaskara nasceu em 1114 na cidade de Bijapur, no atual estado de Karnataka, na Índia. Ele vem de uma família de astrônomos e matemáticos, o que lhe proporcionou um ambiente propício para o desenvolvimento de suas habilidades e interesses nessas áreas.
Durante sua vida, Bhaskara fez contribuições significativas, especialmente em matemática e astronomia. Ele deu a solução mais completa até então para a equação quadrática, que mais tarde ficou conhecida como a “Fórmula de Bhaskara“.
Esta fórmula é um método universal para resolver equações quadráticas, e sua descoberta foi um marco importante na história da matemática.
O legado de Bhaskara perdura até hoje. Seus trabalhos influenciaram não apenas o desenvolvimento da matemática e da astronomia na Índia, mas também em muitas outras partes do mundo.
Vamos agora resolver, Passo a Passo, uma Equação do Segundo Grau: 2x2 – 9x + 7 = 0
Passo 1
Vamos aplicar nosso conhecimento para resolver a equação acima.
Primeiro, identificamos os coeficientes:
- Equação do Segundo Grau: 2x2 – 9x + 7 = 0
- Coeficientes: a= 2, b = -9 e c = 7
Passo 2
Utilizando a Fórmula de Bhaskara, calculamos o discriminante (Δ).
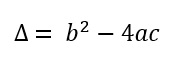
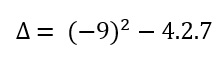
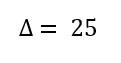
Passo 3
Dando continuidade na Fórmula de Bhaskara, vamos encontrar as raízes de x.
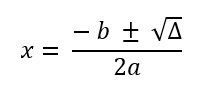
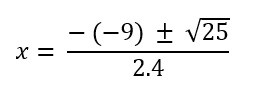
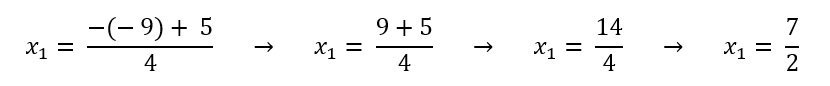
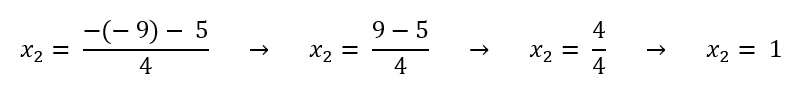
Estes são os valores de x que satisfazem a equação.
Considerações Finais
A equação do 2 grau, apesar de sua aparente simplicidade, é um portal para o entendimento de padrões, relações e fenômenos que moldam nossa realidade. Ela é um exemplo vibrante de como a matemática não está confinada às páginas de um livro didático, mas vive e respira em tudo que nos rodeia.
Cada solução de uma equação do segundo grau é mais do que um mero número; é uma história contada em linguagem matemática, uma narrativa sobre interações e consequências.
Ao compreender esta equação, não apenas melhoramos nossas habilidades analíticas e nossa capacidade de resolver problemas, mas também afinamos nossa percepção do mundo.
Para os estudantes que estão se preparando para o ENEM, lembrem-se: cada equação resolvida é um passo a mais na jornada do conhecimento.
A equação do 2º grau não é apenas um tópico de estudo; ela é uma ponte que conecta a lógica à imaginação, o concreto ao abstrato, e o aprendizado à inovação.
